Calculus 1, part 2 of 2: Derivatives with applications

A total of 56 hours of lectures

This is an academic level course for university and college engineering. Due to its size, it is divided into two parts. This page describes the second of those two parts.

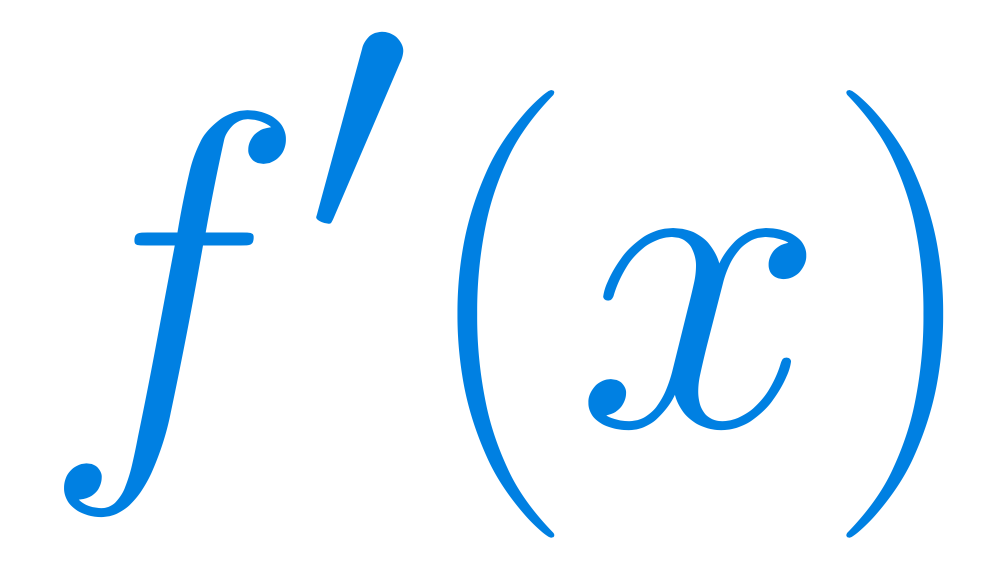
Level - Intermediate

You need to be familiar with the contents of the four Precalculus courses and Calculus 1, part 1 (Limits and continuity) to comfortably follow along in this course.

Curriculum

Make sure that you check with your professor what parts of the course you will need for your exam. Such things vary from country to country, from university to university, and they can even vary from year to year at the same university.

Calculus 1, part 2 of 2

h

Get the outline

A detailed list of all the lectures in part 2 of the course, including which theorems will be discussed and which problems will be solved. If you are looking for a particular kind of problem or a particular concept, this is where you should look first.

Get Calculus 1 part 2 on Udemy

When you buy the course on Udemy, you get access to it for life. There is just a one-time fee. The prices do vary a lot on Udemy, but if you use our link by clicking on this panel, you will get the best current price. See also our page on “coupon codes” in the menu (the current code is TPOT_NOV24).

Course Objectives & Outcomes for part 2

Z
How to solve problems concerning derivatives of real-valued functions of 1 variable (illustrated with 330 solved problems) and why these methods work.
Z
Write equations of tangent lines to graphs of functions.
Z
Prove, apply, and illustrate the formulas for computing derivatives: the Sum Rule, the Product Rule, the Scaling Rule, the Quotient and Reciprocal Rule.
Z
Use the Chain Rule in problem solving with related rates.
Z
Understand the connection between the signs of derivatives and the monotonicity of functions; apply first- and second-derivative tests.
Z
Determine and classify stationary (critical) points for differentiable functions.
Z
Main theorems of Differential Calculus: Fermat’s Theorem, Mean Value Theorems (Lagrange, Cauchy), Rolle’s Theorem, and Darboux Property.
Z
Formulate and prove l’Hospital’s rule; apply it for computing limits of indeterminate forms; algebraical tricks to adapt the rule for various situations.
Z
Classes of functions: C^0, C^1, … , C^∞; connections between these classes, and examples of their members.
Z

Logarithmic differentiation: when and how to use it.

Z
Definition of derivatives of real-valued functions of one real variable, with a geometrical interpretation and many illustrations.
Z
Derive the formulas for the derivatives of basic elementary functions.
Z
Prove and apply the Chain Rule; recognise the situations in which this rule should be applied and draw diagrams helping in the computations.
Z

Use derivatives for solving optimisation problems.

Z
Understand the connection between the second derivative and the local shape of graphs (convexity, concavity, inflection points).
Z
Use derivatives as help in plotting real-valued functions of one real variable.
Z
Formulate, prove, illustrate with examples, apply, and explain the importance of the assumptions in main theorems of Differential Calculus.
Z
Higher order derivatives; an intro to Taylor / Maclaurin polynomials and their applications for approximations and for limits (more in Calculus 2).
Z
Implicit differentiation with some illustrations showing horizontal and vertical tangent lines to implicit curves.
Z
A sneak peek into some future applications of derivatives.

Francisco O.

Udemy student

Well another super course, in this course you have plenty of exercises and theory to handle the difficulty of studying calculus.

So much topics cover in depth even an gentle introduction to implicit differentiation.

Sebastien F.

Udemy student

Excellent course!

Bernard X.

Udemy student

Parfait. merci

Frederick S.

Udemy student

Excellent course. World class.

Jingchao L.

Udemy student

The same impeccable standard as Hania’s other courses!

Ahmet K.

Udemy student

Hania respects the intelligence of her audience and explains mathematics step by step in full detail without resorting to unnecessary simplifications.

A teacher who helps you reach the mathematical maturity you desire over time, without you even realizing it, by establishing constant relationships between all the courses she has created in the past and planned in the future. With these bridges she builds between the past and the future, she motivates you and helps you see the big picture and never forget it.

In mathematics, you cannot say, “Just knowing a little bit of this and a little bit of that is enough for me.” You will know it all. That’s why I took all her courses and continue to do so.

Wanda W.

Udemy student

Great course! Very good explanations, many relevant solved problems and beautiful illustrations.

Richard B.

Lecturer

The logical focus here is the classical quantification of the notion of instantaneous change – through the concept of the derivative of a real variable with respect to another one. The instantaneous change of the location of a particle in physical space is the velocity, we all remember, the derivative of the location with respect to time, and then the instantaneous change of the velocity is the acceleration. Newton’s theory of motion of a material particle, we remember as well, gives us a computational bridge between the description of the motion as the location of the particle in function of time and the description of that motion in terms of the forces that the particle experiences at each moment. Naturally, much like the Newton’s mechanics, the modern mathematical analysis along with its uncounted applications in Science and Technology logically hinge upon the concept of derivative. The students in this Hania’s course are then not only introduced to the technical calculus of derivatives in the thorough spirit of all Hania’s courses, but they also are shown the invaluable intuitive perspective on how to think about the derivative in considerably broader terms.

Maciej G.

Udemy student

A big portion of knowledge given in simple way.

Andrzej P.

Udemy student

This lecture series on Calculus has been excellent, and part 2 covers many important new areas that every student should learn about. As always, the lecturer does a fantastic job at explaining all the topics in an easy to follow manner, with plenty of solved and thoroughly explained exercises included.

Kious

Udemy student

So far so good!